Chapitre 5 La localisation relative

5.1 Introduction

Nous allons proposer dans ce chapitre un cadre d’utilisation des périphériques de pointage à retour de force. Nous avons déjà abordé les limites de ce type de dispositif dans le chapitre 2.

Maintenant, du potentiel du système haptique (voir 1.4, 2.4.3 et 2.6.1), nous pouvons déjà édicter plusieurs règles :

Règle 1 : la précision des doigts en terme de positions, et de mémorisation (Zhai et al., 1996). Ceci implique l’utilisation des périphériques type PHANTOM en mode stylo, de manière à ne pas trop baser l’interaction sur le couple épaule-coude. De plus, une souris peut rester préférable car elle est plus simple à manier en 2D.

Règle 2 : la mémoire sur la position est meilleure que celle sur les distances. (Faineteau et al., 2003)

Règle 3 : l’apprentissage par geste actif donne de meilleurs résultats que celui par geste passif. En d’autres mots, il faudra préférer des phases d’apprentissage de l’interface basées sur l’exploration, plutôt que sur la présentation.

De plus, les modèles de l’utilisateur (en particulier le modèle du processeur humain) nous indiquent quelques règles à respecter sur l’ergonomie des interfaces :

Règle 4 : limiter le nombre d’items de menus

Règle 5 : établir des liens entre éléments (couleurs, format, emplacements) pour faciliter le filtrage cognitif

Règle 6 : écrire des messages concis

Règle 7 : ne pas présenter d’informations inutiles

5.2 La localisation relative

5.2.1 L’idée sous-jacente

C’est grâce à la mémoire sensorielle associée à notre perception kinesthésique, que nous pouvons nous représenter mentalement la position des objets que nous sommes en train de manipuler. Nous allons associer cette approche à une utilisation de périphériques de pointage à retour de force et à un retour audio (synthèse vocale et son). C’est ce que nous nommerons par la suite la localisation relative .

Par exemple, sur la figure 5.1, un utilisateur non-voyant pourra reconnaître les positions relatives de départements français de la région Midi-Pyrénées (l’exemple en haut de la figure) ou bien la disposition des membres d’un être virtuel (l’exemple du bas de la figure).

La localisation relative

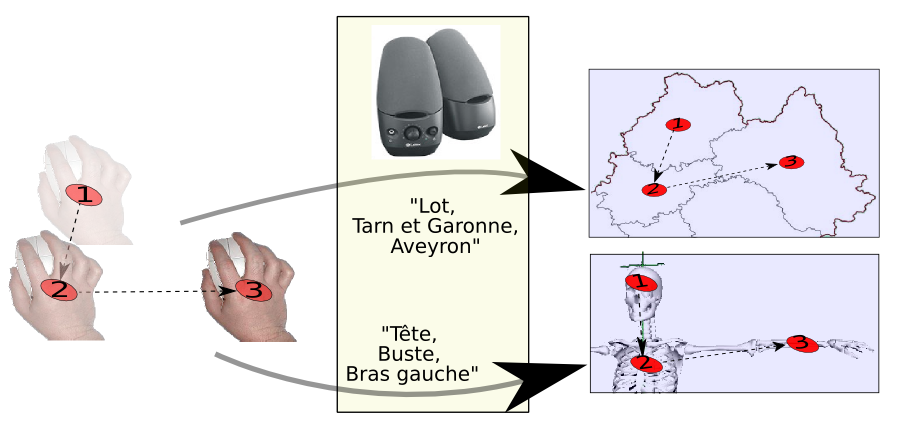
Afin d’illustrer ce concept d’interaction, nous proposons la métaphore du levier de vitesse (figure 5.2)), qui comprend nombre de similitudes avec la localisation relative :

• l’action de l’utilisateur est le déplacement d’un point dans l’espace ;
• le feedback de l’action est constitué par un retour haptique (guidage et cran) et sonore (bruit du moteur) ;
• l’interaction est réalisée sans regarder le levier (ou alors, il faut penser à apprendre à conduire) ;
• une phase d’apprentissage est nécessaire, ainsi qu’une mise à niveau quant aux spécificités des différents modèles. Par exemple, la marche arrière est en haut à gauche, ou encore, la boite compte 6 vitesses.

La métaphore du levier de vitesse

5.2.2 Mise en œuvre technique

5.2.2.1 Cahier des charges

Le système devra respecter au mieux les points suivants :

• Se baser sur des formats de fichier les plus pérennes possible
• Être extensible pour s’adapter à d’autres domaines
• Permettre une traduction haptique la plus automatique possible

5.2.2.2 Le format de fichier

Nous avons décidé de baser notre système sur le formalisme XML. Nous avançons plusieurs raisons à ce choix :

1. Le format XML est un format ouvert et normalisé.
2. Il existe toute une panoplie d’outils pour la manipulation des fichiers XML : XSL, XPath…
3. Certains formats issus du XML peuvent être utilisé dans un contexte Web : SVG, MathML, X3D…

4. Certains domaines disposent de leur formalisme XML

   CML pour la chimie, SVG pour les graphismes vectoriels, MathML pour les mathématiques…

5. Quasiment tous les langages de programmation disposent d’outils permettant la lecture, la manipulation ou la création de fichiers XML. Pour notre part, nous avons utilisé Perl et PHP côté serveur. Côté client, c’était du javascript qui pouvait générer le SVG, javascript parfois lui-même généré par une programmation server-side .
6. Le XML est scriptable . En d’autres mots, il permet une interaction avec l’utilisateur, et ce, de manière relativement facile; de plus, grâce au DOM (Document Objet Manager), il est possible d’agir sur la structure même du document XML, par exemple en ajoutant dynamiquement un objet.

En pratique, c’est le format de fichiers SVG (Scalable Vector Graphics) que nous utilisons. Il s’agit du formalisme XML pour produire des images vectorielles. Mais pourquoi un format qui code des images ? La question est à poser, surtout lorsque les applications basées sur notre approche, ciblent les utilisateurs non-voyants. En fait, le SVG va nous donner les informations spatiales dont nous avons besoin pour générer les effets de retour de force. Et ce, de manière beaucoup plus automatique qu’avec un fichier binaire codant une image bitmap (comme les fichiers jpeg ou gif).

Par exemple, considérons le code SVG suivant :

<rect x="1" y="1"
      width="1198" height="398"
      fill="none" stroke="blue"
      stroke-width="2" />

Il s’agit de la déclaration d’un rectangle dont le coin supérieur gauche est aux coordonnées (1,1), dont la largeur est 1198 et la hauteur 398. En connaissant ces données, il est simple de générer une force sur un périphérique adapté, de manière à amener le dispositif au centre de ce rectangle (en l’occurence, en x=599 et y=296).

5.2.2.3 Le retour de force

Notre retour de force est généré via la souris Wingman Force Feedback Mouse. De plus, nous utilisons le Web Plugin d’Immersion™pour disposer du retour de force dans un navigateur Internet. En l’occurence, il s’agit de Internet Explorer, car c’est un des seuls qui accepte le plugin.

L’effet que nous utilisons pour situer un point haptique est illustré sur la figure 5.3. Il s’agit d’un effet d’encloisonnement elliptique, déclenché lorsque le curseur passe au dessus de certaines zones. Le tout étant de placer judicieusement cet effet, rapport aux coordonnées que nous lisons dans le ficher SVG.

Illustration de l’effet utilisé

5.2.2.4 Une approche manuelle

La première approche que nous avons utilisée pour placer l’effet en relation avec l’affichage, a été purement manuelle. Il s’agissait de créer un tableau contenant les coordonnées des points en question. Ces coordonnées, ont été préalablement relevées, dans un logiciel d’édition de fichiers SVG, à la main. Il fallait de plus, conserver un certain ordre afin de retrouver quelles coordonnées allaient avec quel point.

5.2.2.5 Des approches plus automatiques

5.2.2.5.1 L’emplacement de l’effet est calculé au chargement du SVG :

À la lecture du fichier SVG, il est possible de calculer un couple de coordonnées symbolisant le centre d’une forme. En reprenant notre exemple précédent, qui code le rectangle, une fonction javascript peut facilement calculer le centre de la primitive , en l’occurence, dans le système de coordonnées du SVG, \(x_c=599\), et \(y_c=199\). Nous avons ainsi développé plusieurs fonctions permettant le calcul du centre d’inertie, pour un rectangle, une ellipse.

Le problème s’est compliqué lorsque nous nous sommes penché sur les primitives et . La primitive code une suite de point de la forme “\(x_1,y_1  x_2,y_2... x_n,y_n\)” afin de dessiner un polygone. La primitive dessine un chemin, en donnant par exemple le point de départ, puis une liste de vecteurs. Le calcul en soi du centre d’inertie ne pose pas de problème. Par contre, il est également possible de tomber sur un centre d’inertie extérieur à la forme.

exemple avec la primitive

<polygon points="10,10 10,100 100,100 100,90 20,90 20,50 70,10"
         style="fill: red; stroke: black"/>

La figure 5.4 illustre cette forme, ainsi que le centre d’inertie calculé : \(x_c=47,14\) et \(y_c=137,14\).

Centre d’inertie extérieur à la forme

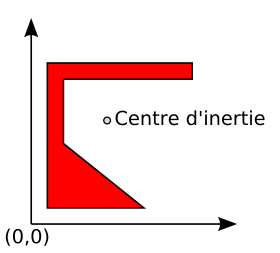
Pour cette raison, et pour éviter d’avoir à se lancer dans de fastidieux calculs qui visent à déterminer le centre géodésique de la forme, nous avons finalement opté pour une autre approche.

5.2.2.5.2 Utilisation de l’attribut translate :

L’approche que nous avons le plus utilisée, est toujours automatique. Néanmoins, elle présuppose un travail préalable lors de la création du fichier SVG; dans notre cas, le travail se fera lors de la génération du fichier.

L’approche consiste en :

1. la création de formes vectorielles, centrée en (0,0),
2. l’utilisation de ces formes en les plaçant dans un fichier SVG. Le placement de ces formes sera réalisé par l’attribut translate

dans l’exemple précédent :

Nous allons centrer la forme en (0,0); cette origine sera le point de retour haptique. Le code suivant

<polygon points="-20,-20 -20,70 70,70 70,60 -10,60 -10,20 40,-20"
         style="fill: red; stroke: black"/>

nous donne la figure 5.5:

Forme centrée sur l’origine

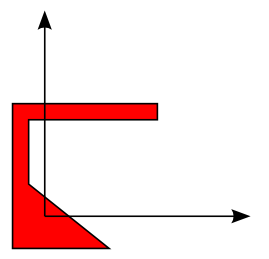
Par la suite, il nous suffira de réutiliser cette forme, en la plaçant grâce à une translate avec la balise adéquate. Par exemple, pour placer notre forme en (50,150), on aura :

Finalement, nous n’avons plus qu’à lire la valeur de la translation pour positionner correctement l’effet. Le gros avantage de cette approche est également sémantique : nous manipulons ici un élément graphique, dont l’origine se trouve être un élément haptique. Notre forme devient un intéracteur bimodal : visuel et haptique.

5.2.2.6 Le retour audio

Dans nos prototypes, le retour audio n’est effectué que d’une seule façon, par sons pré-enregistrés (format wav ou mp3) inclus dans le fichier SVG lors de la génération. Pour autant, d’autres possibilités sont envisageables, telles qu’utiliser un lecteur d’écran et une synthèse vocale, de manière à faire prononcer des mots-clés inclus dans le fichier SVG. Autre approche, de même que nous générons dynamiquement le SVG, il est également possible de synthétiser le retour audio côté serveur, en créant un fichier midi, par exemple.

Enfin, quel que soit la façon dont nous disposons de la modalité audio, cette dernière se déclenche lorsque le pointeur de la souris passe au dessus d’une forme donnée, en même temps que le déclenchement de l’effet haptique.

5.2.2.7 Une architecture client-serveur basée sur MVC

Nous avons choisi un contexte d’application orienté Web-Application. Nos prototypes sont donc basés sur une architecture client-serveur.

Côté serveur, c’est le serveur Web Apache qui est utilisé. Côté client, nous utilisons le navigateur Microsoft Internet Explorer : en effet, Il est actuellement le seul à disposer du support de l’Immersion Web Plugin pour diriger la souris à retour de force.

Architecture du système

Et d’un point de vue logiciel, nous nous sommes appuyé sur l’architecture Modèle-Vue-Contrôleur (MVC). Il s’agit d’un motif de conception pour le développement d’applications logicielles, qui sépare le modèle de données, l’interface utilisateur et la logique de contrôle. Ce motif a été mis au point par (M. H. Reenskaug, 1979), qui travaillait alors sur Smalltalk dans les laboratoires de recherche Xerox PARC.

Ce modèle d’architecture impose la séparation entre les données, les traitements et la présentation, ce qui donne trois parties fondamentales dans l’application finale : le modèle, la vue et le contrôleur :

• Le Modèle représente le comportement de l’application : traitements des données, interactions avec la base de données, etc. Il décrit les données manipulées par l’application et définit les méthodes d’accès.
• La Vue correspond à l’interface avec laquelle l’utilisateur interagit. Elle représente donc l’interaction côte entrée. Les résultats renvoyés par le modèle sont dénués de toute présentation mais sont présentés par les vues. Plusieurs vues peuvent afficher les informations d’un même modèle. Ce sera notre cas, puisque les données que nous afficherons seront diffusées via plusieurs media : l’écran, la souris à retour de force et les haut-parleurs.
• Le Contrôleur prend en charge la gestion des événements de synchronisation pour mettre à jour la vue ou le modèle.

Par extension, et dans un cadre d’utilisation enseignant-élève, nous aurions un système avec un côté enseignant

Le modèle MVC Enseignant-Élève

D’un point de vue technique, le XMLHttpRequest est une fonction javascript invoquée par le contrôleur vers le modèle. L’avantage de cette fonction est qu’elle dispose d’un mode asynchrone, et donc, l’interaction peut continuer côté client, sans attendre la réponse du serveur. C’est ce qui est nommé AJAX pour Asynchronous Javascript And XML (on pourra se référer à l’annexe sur AJAX pour plus de détails).

Les réponses du serveur, enfin, permettent l’extensibilité et la flexibilité de l’application. En effet, deux formes de réponses peuvent survenir :

• la réponse est sous une forme XML : dans ce cas, le contrôleur parse le XML, et en extrait les données nécessaires à l’interaction via la Vue.
• la réponse est sous forme de texte : dans ce cas, le texte peut contenir des commandes pour le contrôleur sur chaque client, commandes pouvant étendre les possibilités du Contrôleur. Par exemple, dans un cadre typiquement enseignant-élève, le contrôleur de chaque poste doit se tenir à jour informé des traitements effectués par le modèle. Une réponse sous forme de texte peut contenir un nouvelle version de la fonction de mise à jour, pour ralentir ces dernières (gestion de la bande passante par le serveur par exemple, si le trafic devient trop important).

5.2.2.8 En résumé

Nous avons présenté notre approche technique. Il faut souligner que le meilleur reste à venir. En effet, pour le moment, le développement reste tributaire du bon vouloir des entreprises : le web plugin d’Immersion Corporation n’est plus développé depuis plusieurs années. Ainsi, il n’est pas possible de l’utiliser sous les navigateurs basé sur Gecko comme mozilla ou firefox. Or, ces navigateurs nous auraient permis d’améliorer la souplesse lors de la programmation, avec par exemple la possibilité d’inclure directement dans le code XML (XHTML en l’occurence) d’une page internet, une partie de SVG, sans avoir besoin de plugin externe pour l’affichage.

Au final, d’ici 2 à 3 ans, les choix techniques discutés ici pourront paraître assez lourds, mais les recommandations conceptuelles resteront valides.

5.2.3 Effet de la nature de la modalité audio sur la mémoire

Nous avons conçu une expérimentation, qui vise d’une part à valider notre approche, mais aussi à démontrer ses limites.

Nous allons chercher à montrer que la nature du retour audio influe sur le temps mis pour explorer une carte haptique, et donc sur la mémorisation de cette dernière. Par nature du retour audio, nous comprenons le type de son : un son contenant un sens écrit , et un son musical. Pour une personne non musicienne, par exemple, il est plus compliqué de mémoriser des notes de musique, que des chiffres, des lettres ou même des phrases.

5.2.3.1 Sujets

Nous avons pu faire passer notre test à 19 personnes (5 femmes, 14 hommes), âgés de 25 à 34 ans. Tous avaient déjà utilisé une souris. Enfin, quatre d’entre eux avait déjà manipulé la souris à retour de force.

5.2.3.2 Matériel

Le test a été effectué à l’aide de la souris Wingman Force Feedback Mouse. Pour le reste, une architecture client-serveur était en place, à savoir un serveur Apache, avec PHP activé, et un client avec Microsoft Internet Explorer pour lire les données envoyées par le serveur. Dans notre cas, le serveur et le client tournaient sur la même machine, un portable équipé de 512 Mo de mémoire, et d’un processeur Pentium 4 à 2 Ghz. Enfin le retour sonore se faisait via un casque audio.

5.2.3.3 Procédure

La tâche que nous avons mise au point est la plus générique possible. Il s’agit de compter des points haptiques à l’aide de la souris Wingman et sans retour visuel. Un point haptique est un effet d’attirance en un certain endroit de l’espace de travail de la souris.

L’espace de travail de la souris est ainsi divisé en un certain nombre de régions. Chaque région est donc pourvue d’un retour de force (un point haptique), et d’un retour sonore. Nous avons utilisé différents retours sonores, à savoir, des notes de musique, des lettres de l’alphabet pré-enregistrées, et le silence.

Les différents paramètres de l’expérience sont précisés dans le tableau 5.1.

Table 5.1: Les conditions expérimentales

Conditions audios :	Notes, Lettres, ou Silence
Nombre de régions à trouver :	3, 6 ou 9

La répartition des points haptiques sur la surface de travail de la souris est générée par une programmation côté serveur, de manière à construire des fichiers SVG, eux-mêmes interprétés, par une programmation javascript côté client, afin de générer le retour de force. Enfin, les positions de ces points haptiques sont choisies lors de la génération, parmi 18 positions pré-établies. À noter, enfin, que l’espace non-occupé par les formes SVG, génère une vibration avec la souris, indiquant au sujet qu’il est sorti de la zone d’intérêt. La figure 5.8 montre quelques configurations que les sujets ont dû explorer.

Exemples des configurations à explorer ; les hexagones colorés représentent les zones haptiques à trouver et et à localiser

Une session consiste en une phase d’exploration avec 3, 6 ou 9 points haptiques, et une des conditions audios. Les sessions sont chronométrées. Et à la fin de chaque session, deux questions sont posées au sujet :

1. Combien y-a-t-il de points haptiques ?
2. Comment sont-ils agencés les uns par rapport aux autres ? (question ouverte : nous n’avons pas utilisé de formulaire de réponse, mais nous avons consigné les réponses orales, écrites ou gestuelles)

L’ordre des différentes sessions selon le nombre de points, et le type de retour audio, est aléatoire. Ceci afin de limiter les effets de l’apprentissage d’une session à l’autre, par rapport à la difficulté de la tâche (c’est à dire le nombre de points à trouver).

Avant de commencer, un exemple de chaque condition sonore est proposé, afin d’habituer les sujets au maniement de la souris, et au déroulement du test.

Pour terminer, nous avons noté les remarques que les sujets pouvaient nous faire.

5.2.3.4 Résultats et Discussion

5.2.3.4.1 Le temps nécessaire pour compléter la tâche : la mémorisation

La première donnée mesurable que nous pouvons commenter est le temps mis pour achever la tâche, en fonction du nombre de points et de la nature du retour audio. Le tableau 5.2 nous indique ces résultats, que la figure 5.9 illustre.

Table 5.2: Moyennes des temps (en ms), selon les conditions audios (axe horizontal) et le nombre de points (axe vertical)

	Notes	Lettres	Silence	Moyenne
3 points	55,8	48,9	56	53,6
6 points	117,6	87,6	144,4	116,5
9 points	162	117,4	183,1	154,2
Moyenne	111,8	84,7	127,8	108,1

Les temps selon les différentes conditions audios

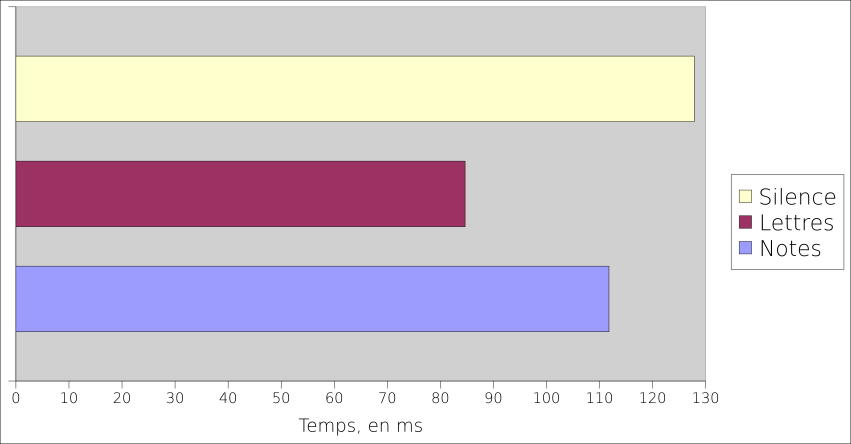
Nous remarquons immédiatement que les performances sont nettement meilleures avec les lettres. En moyenne, la tâche avec les notes de musique est 31,8% plus lente qu’avec les lettres ; et la tâche sans retour audio est 50,8% plus lente.

À présent, la figure 5.10 présente ces mêmes résultats, en les groupant selon le nombre de points présentés.

Les moyennes des temps, selon les différentes conditions audios, et en fonction du nombre de points à trouver

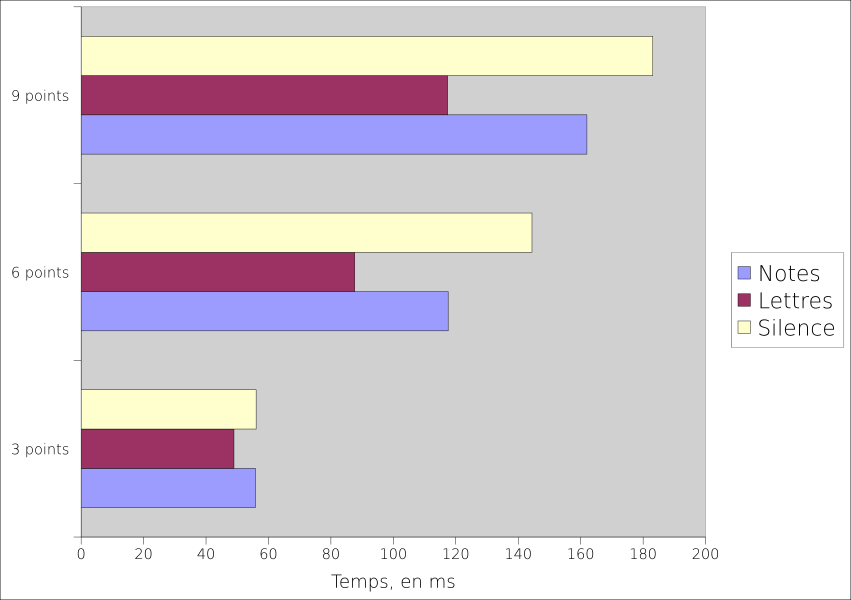
Les temps évoluent clairement en augmentant avec le nombre de points, et ce d’une manière pratiquement linéaire. De plus, on retrouve un comportement très similaire dans les trois cas : la reconnaissance est plus rapide quand ce sont des lettres qui sont présentées, puis viennent les notes de musique, et le silence.

Petite remarque, néanmoins : lorsqu’il n’y a que trois points, les différences de performances sont relativement faibles (de l’ordre de 15%). On peut expliquer ceci par le fait que trois éléments à mémoriser reste de toute façon une tâche facile, même si on remarque déjà des différences de performance.

5.2.3.4.2 La mémorisation de l’agencement spatial

Grâce aux questions posées après chaque essai, nous avons pu noter sur 10, la qualité de l’agencement reconnu des points.

La note est calculée de la manière suivante :

1. la première réponse concerne le nombre de points reconnus. Sur cette partie, on notera *N**c* le nombre reconnu de points, et *N**r* le nombre réel de points. L’ensemble de la note devra tenir compte du nombre d’éléments à retrouver *N**r* : en effet, il serait étrange de sanctionner d’avantage 7 points trouvés sur 9 , que 2 points trouvés sur 3 .
2. la seconde réponse concerne l’agencement des points. La note est ici plus difficile à formaliser afin d’éviter une certaine subjectivité : nous devons compter avec la disposition générale des réponses données (il y a un élément en haut, et un autre à droite ), ainsi qu’avec une certaine exigence de précision (l’élément du haut est deux fois plus éloigné du centre que celui de droite ). Nous notons cette partie de la note \(a\)g, entre 0 et 10.

Nous allons chercher à obtenir une note N, sur 10, dans tous les cas de figure (3, 6, et 9 points). Le comportement de la notation doit suivre la qualité de la réponse.

La note N sera alors calculée selon la formule :

\[ N=A\_{g}\left(\frac{N\_{c}}{N\_{r}}\right)\]

Ce comportement de la notation nous semble conforme à la qualité des réponses.

Au final, le tableau 5.3 présente la synthèse de ces notes, et la figure 5.11 illustre le comportement des notes, selon la nature du retour audio.

Table 5.3: Moyennes des notations, sur 10, selon les différentes conditions audios, et en fonction du nombre de points à trouver

	Notes	Lettres	Silence	Moyenne
3 points	9,48	9,75	9,18	9,48
6 points	7,28	8,03	6,33	7,21
9 points	5,33	6,82	4,98	5,71
Moyenne	7,39	8,20	6,83	7,46

Notations selon les différentes conditions audios

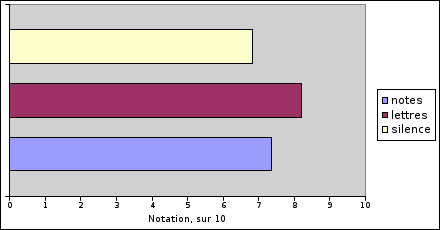
D’une manière similaire à ce que l’on a observé avec les temps, au paragraphe précédent, nous notons que le retour Lettres obtient les meilleures notes. Le retour audio notes obtient des notes 9,5% plus faibles que le retour lettre ; quant au retour silence , ses notes sont 16,7% plus faibles.

Nous notons également que les notes s’effondrent très rapidement avec l’augmentation du nombre de points à découvrir. Cela peut provenir de notre méthode de notation, mais nous pensons qu’il s’agit de la difficulté intrinsèque de la tâche : une reconnaissance, et une localisation à l’aide d’une souris à retour de force, reste une tâche ardue, du fait notamment du manque de précision du périphérique, et du retour haptique sur un unique point de contact.

Maintenant, la figure 5.12 distingue les notes selon le nombre de points à découvrir.

Notations, selon les différentes conditions audios, et en fonction du nombre de points à trouver

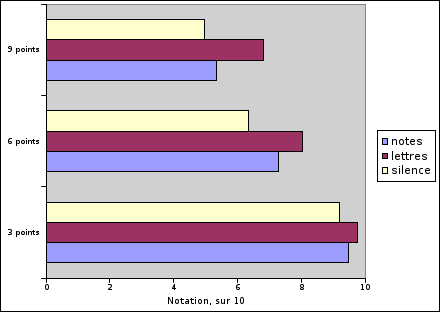
Là encore, les résultats sont très proches de ceux déjà observés, et ce, dans les trois cas de figure : les meilleurs résultats pour le retour lettres , suivi du retour notes , et le retour silence .

Il s’agit maintenant de commenter tous ces résultats, ensembles. À savoir, existe-t-il un lien entre les performances lors de la tâche, et la note obtenue ?

5.2.3.4.3 Corrélation entre le temps de la tâche et la notation ?

Pour terminer, nous synthétisons tous ces résultats sur la figure 5.13.

Corrélation entre le temps mis lors de la tâche, et la notation. Les grands symboles représentent les positions moyennes pour chacune des conditions de retour audio

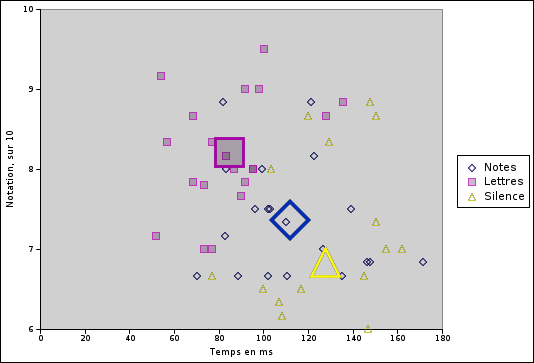
5.2.3.5 En conclusion

Cette série de tests nous permet de poser quelques réflexions sur notre approche. Cela montre déjà la faisabilité de l’approche : la mémorisation s’opère bien, et les erreurs quant-à la précision spatiale tend à diminuer avec l’habitude du dispositif.

Les retours utilisateurs désignent cependant les limites du périphérique. Bien que l’approche plaise lors de l’explication pré-expérimentation, il s’ensuit une certaine frustration : les effets ne sont pas assez forts . Ceci est malheureusement le fait des caractéristiques techniques de la souris, plafonnant à 1N.

Nous pensons que cela peut néanmoins valider notre approche, tout du moins dans un cadre d’expérimentation et de prospection.

Par la suite, un test impliquant plus de monde pourrait permettre d’affiner les résultats. Il pourrait être intéressant, par exemple, de prendre en compte l’effet de l’âge sur les résultats. Les données que nous avons recueillies ne sont pas suffisamment nombreuses pour pouvoir conclure sur ce point, mais il semble que les sujets jeunes appréhendent plus facilement, et rapidement, le maniement de la souris.

5.2.4 Modélisation du temps d’exploration

Nous allons maintenant tenter de modéliser le temps qu’il nous faut pour explorer une surface haptique, telle que nous la considérons depuis le début de ce chapitre. L’idée est de déterminer comment le temps d’exploration évolue, en fonction du nombre d’éléments présentés. Enfin, l’expérience précédente semble avoir montré une évolution du temps d’exploration linéaire, selon le nombre d’éléments à sentir.

Nous allons donc proposer une tâche de recherche d’éléments, parmi un ensemble de points haptiques.

Nous posons l’hypothèse que le temps \(T\) de la tâche peut se décomposer de la manière suivante :

\[\begin{equation} T=ET+RT+MT\label{eq:temps}\end{equation}\]

avec, \(T\), le temps total de la tâche,

\(ET\), le temps d’exploration

\(RT\), le temps de réaction

et \(MT\), le temps du mouvement.

Ce dernier sera modélisé selon la loi de Fitts. Le temps de réaction \(RT\) sera modélisé selon la loi de Hick-Hyman, que nous présentons maintenant.

5.2.4.1 La loi de Hick-Hyman

Hick et Hyman (Hyman, 1953) on étudié la relation entre le temps de réaction \(RT\) et le nombre de réponses-stimuli alternatifs n. Leurs résultats montrent que le choix \(RT\) semble augmenter régulièrement d’environ 150 ms lorsque le nombre de réponses-stimuli n double. Ceci suggère une relation logarithmique entre le nombre de stimuli-réponses et le temps de réaction. L’interprétation de cette relation montre que le logarithme du nombre d’alternatives est une mesure de la quantité d’information à traiter. Plus il y a d’alternatives, plus il y a d’informations à traiter.

La loi de Hick-Hyman s’exprime ainsi :

le temps de réaction pour faire un choix parmi n alternatives est :

\[\begin{equation} RT=a+b\log_2(n)\label{eq:hick}\end{equation}\]

où \(a\) et \(b\) sont des constantes déterminées empiriquement.

\(b\) est la pente ou le taux de traitement d’information et s’exprime en s/bit. Généralement, \(b=127−215\) ms/bit d’information.

\(a\) est l’ordonnée à l’origine et est exprimé en secondes. On estime \(a=179\) ms lorsque \(log_2(n)=0, n=1\). Ainsi, \(a\) est la vitesse élémentaire du système de perception moteur.

Les valeurs de \(a\) et \(b\) dépendent :

• de l’entraînement;
• de l’effet de compatibilité entre les stimuli et les réponses;
• de la familiarité avec le sous-ensemble de stimuli;
• du pouvoir de discrimination entre les stimuli;
• et de l’effet de la répétition des stimuli.

5.2.4.2 Sujets

Onze sujets, âgés de 24 à 32 ans, ont participé au test. Tous avaient déjà participé au test précédent, et donc, avaient une certaine habitude avec la souris à retour de force.

5.2.4.3 Matériel

Le présent test reprend exactement le même matériel que le précédent. À savoir : une souris à retour de force Wingman Force Feedback Mouse, branchée sur notre architecture client-serveur; des script php générant les médias.

5.2.4.4 Procédure

La tâche demandée aux sujets est la suivante :

Un certain nombre de points haptiques vont vous être présentés à l’aide de la souris à retour de force. À chaque point est associé un retour audio; ici, ce sera un nombre qui sera lu. Vous devez explorer la surface, puis aller cliquer le plus vite possible sur la zone dont le retour audio correspond au nombre le plus faible.

Visuellement, la tâche peut être représentée comme indiqué sur la figure 5.14. Cependant, lors de ce test, l’écran n’était pas allumé.

Illustration de la procédure, pour 4 points

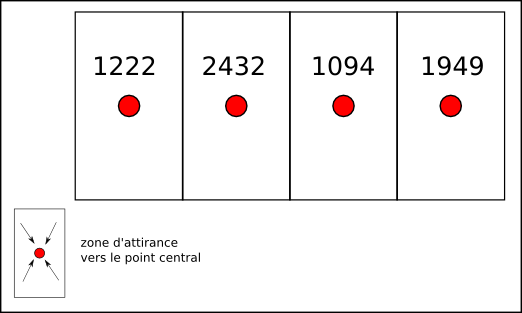
Synthétiquement, les conditions expérimentales se trouvent dans le tableau 5.4. Ainsi, à chaque session de l’expérience, le nombre de points haptiques augmente. On commence avec 2 points ; puis 3, 4, 6, et enfin 9 points. Chaque session comporte 10 essais, où les valeurs des nombres lus, et leurs positions, sont tirés aléatoirement. Enfin, ces nombres sont lus par une synthèse vocale; leurs valeurs varient entre 1000 et 3000. Les sujets ne sont pas au courant de ces bornes.

Table 5.4: Paramètres de l’expérience

Nombre de zones	2, 3, 4, 6 et 9
Valeurs des nombres	[1000;3000]
nombre d’essais par session	10

5.2.4.5 Calcul du temps théorique moyen des mouvements

Afin de déduire le temps d’exploration \(ET\), nous allons soustraire au temps total le temps de réaction \(RT\), que nous obtenons grâce à la loi de Hick-Hyman, ainsi que le temps du mouvements \(MT\).

Comme dans chaque situation, la position de la cible à atteindre est aléatoire, nous allons estimer la moyenne des mouvements possibles, en fonction du nombre de zones.

Détaillons le calcul pour 4 zones. La situation est schématisée sur la figure 5.15.

Les mouvements possibles pour 4 zones à explorer

Nous dénombrons :

• 4 mouvements nuls
• 6 mouvements d’une longueur \(a/2\)
• 4 mouvements d’une longueur \(3a/2\)
• et 2 mouvements d’une longueur \(5a\)

Soit, respectivement, et d’après la loi de Fitts, des temps de mouvements équivalents à:

• \(4a\) ms
• \(6\left[a+\log_{2}\left(\frac{A}{2W}+1\right)\right]\) ms
• \(4\left[a+\log_{2}\left(\frac{3A}{2W}+1\right)\right]\) ms
• \(2\left[a+\log_{2}\left(\frac{5A}{2W}+1\right)\right]\) ms

Tous ces calculs sont théoriques. Pour obtenir une valeur numérique, nous allons utiliser les valeurs des coefficients que nous avons déterminés lors de l’expérience sur les performances d’une tâche de pointage sur un champ à retour de force (voir cha :=C9valuation-des-performances), à savoir 380 ms., et \(b\)=123 ms/bit (condition MTDF).

Il nous reste alors à déduire la moyenne des temps, en fonction du nombre de zones. Les résultats des calculs sont dans le tableaux 5.5.

Table 5.5: Temps théoriques des mouvements moyens, en fonction du nombre de zones

n	2	3	4	6	9
\(MT_{moy}\) (en ms)	499	528	550	586	627

5.2.4.6 Calcul du temps de réaction théorique

En s’appuyant sur la loi de Hick-Hyman, nous pouvons écrire les temps théoriques minimum et maximum de réaction, avec les coefficient \(b−=127\) ms/bit., et \(b+=215\) ms/bit.

• minimum : \[\begin{equation} RT^{-}(n)=179+127\log_{2}(n) \tag{5.1} \end{equation}\]

• et maximum : \[\begin{equation} RT^{+}(n)=179+215\log_{2}(n) \tag{5.2} \end{equation}\]

D’où l’évolution des temps théoriques minimum et maximum de réaction, en fonction du nombre de zones (tableau 5.6).

Table 5.6: Temps de réaction minimum et maximum théoriques

Nombre de zones	2	3	4	6	9
Temps de réaction minimum \(RT^{-}\) (ms)	306	380	433	507	581
Temps de réaction minimum \(RT^{+}\) (ms)	394	519	609	734	860

5.2.4.7 Résultats et discussion

Les résultats de l’expérience sont présentés dans le tableau 5.7, et illustrés graphiquement sur la figure 5.16.

Table 5.7: Résultats de l’expérience

Nombre de zones	2	3	4	6	9
Temps moyen de la tâche (ms)	1291	2269	2636	4869	5644

Évolution du temps de la tâche en fonction du nombre de zones

En partant de notre hypothèse de base, c’est à dire \(Temps=ET+RT+MT\), nous pouvons déduire les valeurs minimum et maximum des temps d’exporation \(ET^{-}\) et \(ET^{+}\), en soustrayant aux temps de la tâche, les temps théoriques de réaction (\(ET^{-}\) et \(ET^{+}\) calculé avec les équations (5.1) et (5.2)), ainsi que les temps théoriques moyens des mouvements \(MT^{moy}\). Ce calcul est synthétisé dans le tableau 5.8.

Table 5.8: Résultats : les temps moyens de la tâche \(T\), les temps théoriques \(MT\), et \(RT\), d’où par soustraction les temps d’exploration minimum et maximum \(ET^{-}\) et \(ET^{+}\).

Nombre de points	Temps (empiriques)	\(RT^{-}\) (théoriques)	\(RT^{+}\) (théoriques)	\(MT^{moy}\) (théoriques)	\(ET^{-}\) (déduits)	\(ET^{+}\) (déduits)
2	1291	306	394	499	486	398
3	2269	380	519	528	1361	1222
4	2636	433	609	550	1652	1476
6	4869	507	734	586	3776	3548
9	5644	581	860	627	4435	4156

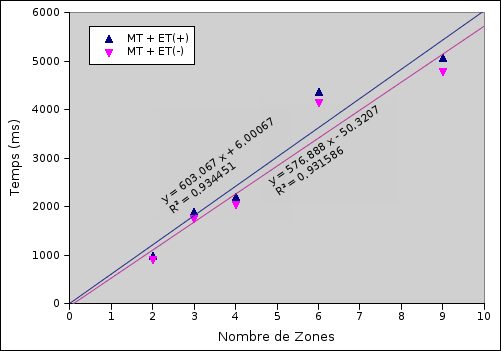
Traçons maintenant, la somme des temps de mouvement et d’exploration : on a soustrait des temps totaux, le temps de réaction théorique. On peut d’ores et déjà noter, sur la figure 5.17, que dans ce cas, le temps tombe à 0 quand le nombre de zones est nul. Ceci tend à confirmer notre hypothèse de départ. En effet, une fois ôté le temps de réaction, le temps devrait se trouver nul, car il n’y a plus, ni exploration, et donc ni mouvement. À noter qu’avec une cible unique, le temps \(MT\)+\(ET\) est non nul. Cela provient du temps de déclenchement du geste (le terme \(a\) dans la loi de Fitts).

Temps d’exploration et de mouvement, en fonction du nombre de zones

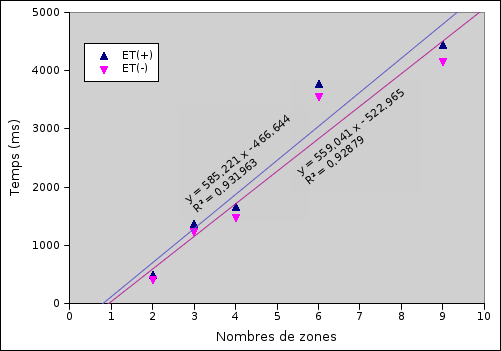
Soustrayons à présent le temps de mouvement \(MT\), et traçons le résultat sur la figure 5.18. Nous pouvons y observer que le temps d’exploration \(ET\), tombe à 0 lorsqu’il n’y a qu’une seule zone haptique. Ceci tend également à confirmer notre hypothèse. En effet, on peut imaginer qu’avec une seule zone, il n’y a intuitivement pas de phase d’exploration.

Temps d’exploration en fonction du nombre de zones

5.2.4.8 Conclusion

D’après notre expérimentation, le temps d’exploration d’une surface, à la recherche d’une zone haptique, semble être linéaire en n. Cependant, notons bien que dans notre test, nous n’avons pas étudié les cas au delà de 9 points haptiques. En effet, le modèle du processeur humain nous donne une mémorisation à court terme de 7±2 éléments, selon la concentration ou la fatigue. Aussi, nous essaierons d’éviter de présenter trop de zones haptiques en même temps, dans une tâche de mémorisation.

5.2.5 Vers les applications de la localisation relative

Les tests que nous avons effectués dans cette section, valident selon nous notre approche, en terme de mémorisation sensorielle, ainsi qu’en terme d’utilisation du dispositif. Passé la surprise lors des premiers maniements de la souris à retour de force, les sujets de nos tests ont tous relevé l’intérêt d’un tel dispositif, tout en regrettant parfois la surface de travail trop petite.

Nous allons maintenant poursuivre dans ce chapitre en présentant les deux prototypes basés sur la localisation relative, que nous avons développés. Le premier prototype concerne la géographie, et le second, l’harmonie musicale.

5.3 Application à la géographie : geogr’haptique

Géogr’haptique est une application de la localisation relative, dans laquelle les points haptiques sont les centres des régions d’un pays, et le retour audio, la diction (pré-enregistrée ou par une synthèse vocale) du nom de cette région.

5.3.1 Ce dont disposent les non-voyants pour avoir accès aux cartes géographiques

La première solution dont une personne aveugle dispose pour appréhender la géographie, consiste à prendre un atlas géographique traduit en braille. Il lui faudra alors se faire une image mentale de la carte, en parcourant le texte. Du fait de la distance cognitive entre la représentation textuelle et la représentation spatiale, cela s’avère difficile, et assez peu parlant quant à la forme, la taille et la disposition géographique des pays, des régions, des villes ou des rivières.

Une autre possibilité consiste à utiliser des cartes tactiles. Ces dernières font apparaître les frontières, les découpages administratifs, les villes, de la même manière que des cartes conventionnelles. Cette fois, il y a une correspondance directe, à un facteur d’échelle près, entre l’information et la représentation. Cette méthode amène donc un contact direct avec la nature géographique de l’information : superficies, formes, emplacements.

Le projet CDV (pour Cartographie pour Déficients Visuels¹²), au Canada, (Siekierska et al., 2001) propose l’accès à des cartes prêtes à imprimer en se servant d’un amplificateur thermique : la représentation graphique (figure 5.19) est téléchargée, imprimée sur du ” papier-capsule ” et passé dans un amplificateur thermique. Le papier-capsule, un papier qui gonfle sous l’effet de la chaleur, est utilisé dans un copieur stéréoscopique pour mettre en relief les surfaces imprimées telles que les courbes de niveau, les poncifs et l’information textuelle.

Représentation graphique d’une carte tactile. Dans cet exemple, il s’agit des différents types de forêts du Canada

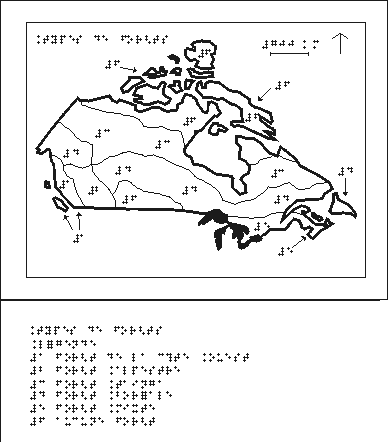
Des projets pédagogiques dédiés aux non-voyants ont été mis sur pieds, comme le projet TactiSon. TactiSon a été développé par l’INSERM-Creare et le CNEFEI (Centre National d’Etudes et de Formation pour l’Enfance Inadaptée) pour servir de support d’enseignement à des personnes handicapées visuelles à partir de la maternelle jusqu’à la fin des études supérieures. Mais il peut aussi constituer un support d’information et d’orientation spatiale. D’abord utilisé pour éveiller l’enfant puis pour aborder des notions scolaires, TactiSon sert aussi bien de support pour la représentation de graphiques mathématiques, de cartes de géographie, de plans de villes, de quartiers, de bâtiments publics.

Le principe est le suivant : on place une feuille avec le document graphique en relief que l’on souhaite étudier, sur un dispositif relié à un PC. Il est alors possible de définir des zones sensibles auxquelles on affecte une action. Par exemple, couplé à une synthèse vocale, les différents points du graphique peuvent déclencher des messages vocaux. En posant le doigt sur une région, on entendra le nom de cette région, et éventuellement d’autres informations. Pour la géographie, TactiSon permet d’enrichir des cartes géographiques et des plans de villes sans les surcharger de texte braille souvent encombrant.

Enfin, le CDV, encore, propose une application des travaux de (Gardner and Bulatov, 2001). Il s’agit d’un environnement qui permet de lire des carte SVG relativement simples, et de les augmenter avec le mode haptique : sensation des frontières et des formes des régions.

5.3.2 L’application Géogr’Haptic

L’application que nous avons conçue a pour but de permettre à un utilisateur non-voyant de se faire une image mentale d’une carte géographique. A l’écran, est affichée une carte d’un pays indiquant ses différentes régions administratives. L’utilisateur se sert de la souris pour parcourir l’écran. A chaque fois qu’il passe au-dessus d’une région, un retour kinesthésique place la souris en son centre. En même temps, le nom de la région est lu par un lecteur d’écran et une synthèse vocale, pour assurer un retour sonore.

Geogr’haptique est une application orientée Internet. Ceci implique qu’elle tourne sur un classique navigateur Internet comme Internet Explorer ou Netscape Navigator. L’ensemble de la carte réagit comme une image réactive déclarée avec la balise

Pour fonctionner, il est toutefois nécessaire d’avoir installé deux plugins pour le navigateur Internet que l’on utilise :

• Le plugin ImmWeb d’Immersion Corporation qui autorise une programmation Javascript des effets haptiques de la souris.
• Le plugin SVGViewer d’Adobe, pour afficher les fichiers SVG. Ces fichiers sont la base graphique de l’application. Ce sont eux qui contiennent toute l’information graphique des cartes.

5.3.3 Géogr’haptique en action

Nous allons maintenant illustrer le fonctionnement de Géogr’haptique :

Situation de départ : une carte des Etats-Unis est affichée dans le navigateur internet. Le pointeur de la souris se trouve sur l’état du Kansas. Le son « Kansas » vient de sortir du haut-parleur et la souris semble aimantée dans sa position actuelle (figure 5.20).

Géogr’haptique, situation initiale

Maintenant, on saisit la souris, et on la pousse vers la gauche. Il faut un peut forcer car elle nous ramènerait inexorablement vers le point d’origine. Pourtant, un instant plus tard, la force ressentie dans la souris s’est inversée, le périphérique se stabilise dans une nouvelle position située à gauche de la précédente et le mot « Colorado » vient d’être prononcé par la synthèse vocale (figure 5.21).

Géogr’haptique, situation finale

5.3.4 Au final

Nous avons pu faire tester notre prototype de manière informelle par quelques personnes non(ou mal)-voyantes. Il leur a été par exemple demandé de citer les régions frontalières à une région donnée, et cette tâche a été facilement réalisée. Comparé à l’utilisation de la balise

Tous nos testeurs ont donc souligné l’intérêt de l’approche, tout en regrettant de ne pas disposer d’un accès à une information géographique plus large, comme c’est par exemple le cas sur des web-services (non-accessibles cependant aux non-voyants) comme Google Maps¹³, Yahoo Local¹⁴, ou encore MSN Virtual Earth¹⁵.

La viabilité de notre approche est tout de même clairement apparu, et nous avons pu nous tourner vers un autre domaine : la musique.

5.4 Application à la musique : Music’Haptic

Dans cette partie, nous présentons Music’Haptic, un prototype d’application d’enseignement de la musique, via la découverte des notes et des accords. Le retour audio de la localisation relative sera évidement des notes de musique. Pour les points haptiques, nous allons avoir besoin d’une notation spatiale de l’information musicale.

5.4.1 Spatialisation de l’information musicale et apprentissage

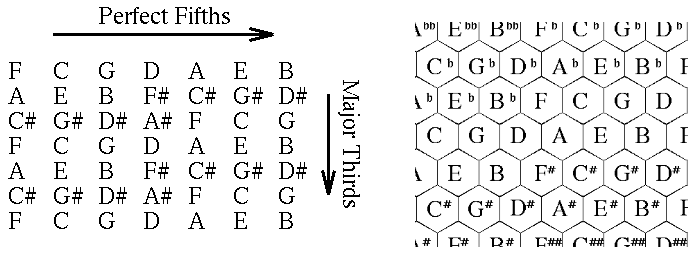
La théorie de l’harmonie de Longuet-Higgins (Longuet-Higgins et al., 1962) (Longuet-Higgins, n.d.) propose l’utilisation d’un tableau de notes. La représentation de Longuet-Higgins a été un des premiers cadres théoriques permettant d’expliquer la perception et les traitements cognitifs mis en œuvre lors de l’écoute harmonique. La théorie de Longuet-Higgins (Longuet-Higgins et al., 1962) (Longuet-Higgins, n.d.) affirme que les intervalles qui interviennent dans la musique tonale occidentale sont ceux entre les notes dont la fréquence peut s’exprimer comme produit des trois facteurs principaux 2, 3, et 5 et aucun autre. Une fois assimilé cette assertion, il s’ensuit que l’ensemble constitué des intervalles de l’octave (8 tons), de la quinte juste (5 tons) et de la tierce majeure (3 tons) est le seul système de coordonnées capable de représenter une note quelconque de manière unique (selon un triplet de valeur suivant les trois axes). Ceci peut être représenté graphiquement en rangeant les notes dans une grille en trois dimensions, selon les tierces, les quintes et les octaves. Enfin, il est fréquent d’ oublier de noter l’octave, du fait de l’équivalence entre deux notes séparées par cet intervalle, afin de se concentrer sur les deux autres dimensions : les quintes justes sont alors sur un axe et les tierces majeures sont sur l’autre (figure 5.22).

Plus tard, (Steedman, 1972) a proposé une notation dérivée de celle de Longuet-Higgins et nous la détaillerons dans la prochaine section.

Représentations de Longuet-Higgins (à gauche) et de Steedman (à droite)

La théorie de Longuet-Higgins a été très étudiée en psychologie cognitive de la musique (Howell et al., 1985) en tant que cadre pour expliquer comment s’effectuait la perception et le traitement de l’harmonie tonale. Plus tard, cette théorie a été appliquée pour développer de nouveaux outils éducatifs pour la musique. Par exemple, les travaux de Holland (Holland, 1987) (Edwards and Holland, 1992) sont basés sur la notation de Longuet-Higgins afin de produire des interfaces interactives dans lesquelles les notes, les intervalles, les accords, les cadences ou les modulations, peuvent être directement manipulées et visualisées, grâce à une métaphore spatiale.

L’ordinateur a beaucoup été utilisé pour l’apprentissage de la musique. Et comme résultante de la nature pluridisciplinaire du domaine, les approches employées peuvent être très différentes. On pourra se référer à (Brandao et al., 1999) pour une étude exhaustive des techniques employées.

Plusieurs contextes ont été employés dans ces tâches :

• la visualisation graphique : (Holland, 1987) et (Castaing, 2005)
• l’intelligence artificielle : (Holland, 2000)
• l’analyse et la composition assistée par ordinateur

Pour autant, ces approches oublient souvent les utilisateurs ayant une déficience visuelle. L’accessibilité à la notation musicale pour les personnes non-voyantes, est généralement basée sur la transcription linéaire de la partition, en Braille. Les applications informatiques (“Braille music editor,” n.d.) et (“Toccata - braill music translation software,” n.d.) fonctionnent de cette façon. Mais cela implique la connaissance préalable des notions musicale et harmoniques, ainsi que du Braille musical.

5.4.2 La représentation de Steedman

Comme nous venons de le voir, selon la théorie de Longuet-Higgins, tous les intervalles de la musique tonale peuvent être représentés comme une combinaison d’octave, de quinte juste et de tierce majeure.

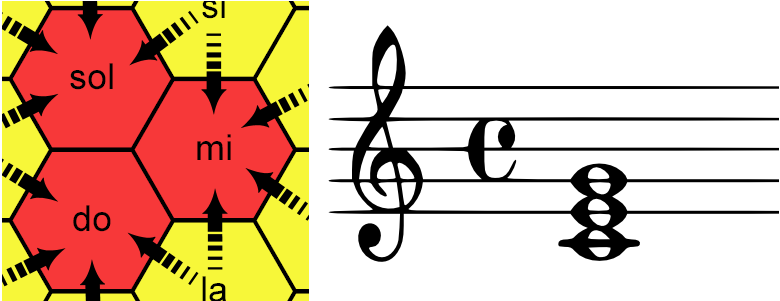
Mark (Steedman, 1972) a proposé une autre notation, en décalant les lignes de l’espace, de manière à pouvoir intercaler les tierces mineures dans le plan. On se retrouve maintenant avec six voisins par notes, et donc, avec une représentation hexagonale (figure 5.23).

La représentation de Steedman et ses trois axes harmoniques

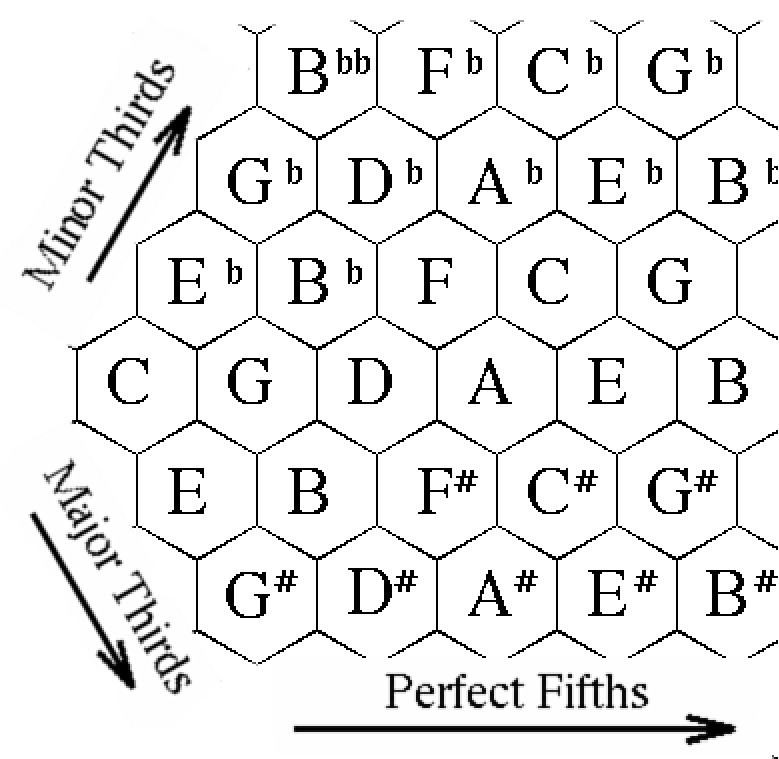
Nous avons choisi cette notation, pour lui appliquer la localisation relative. En effet, par rapport à la notation de Longuet-Higgins, les voisins d’une note sont équidistants. Donc, la loi de (Fitts, 1954) nous donne un temps égal pour accéder à chacun de ces voisins. De plus, ces six notes voisines peuvent être considérées comme étant les notes les plus harmoniquement proches de la note centrale.

Par rapport à la représentation originale, nous avons procédé à une rotation de 90 degrés dans le sens direct, de manière à préserver la corrélation intuitive que l’on peut avoir entre la hauteur du son (sa fréquence), et la direction à l’écran : plus la position est haute sur l’écran, plus le son a une fréquence élevée.

Les principales caractéristiques de notre représentation (figure 5.23) sont :

• l’axe vertical est constitué d’un empilement de quintes justes. Une des caractéristiques de cet intervalle se retrouve : en parcourant les notes sur cet axe, on passe successivement par toutes les notes, avant de reboucler au bout de 12 notes.
• l’axe diagonal allant vers le haut à droite, est constitué des tierces majeures. De manière similaire à ce que l’on a pour les quintes justes, il y a un comportement cyclique, et on retombe sur la même note au bout de 3 notes.
• l’autre axe diagonal contient les tierces mineures. Son cycle fait 4 notes de long.

La représentation de Steedman, telle qu’elle est implémentée

La plus importante des caractéristiques de cette notation (et de celle de Longuet-Higgins) est la suivante : un accord est constitué de plusieurs notes jouées en même temps. Sur la représentation, on peut noter un accord en ne gardant que les notes jouées. Il se trouve qu’en notant les principaux accords de la musique occidentale, on trouve des formes spécifiques; qui plus est, ces formes ne varient pas avec la tonalité de l’accord. La figure 5.25) montre les accords que nous considérons. Il faut bien garder à l’esprit que ces formes (par exemple le triangle isocèle pointant vers la droite pour la quinte majeure) restent les mêmes quelle que soit la tonalité de l’accord.

Nous allons nous baser sur cette propriété pour créer un outil d’apprentissage des accords, pour un utilisateur non-voyant. En effet, après une phase d’apprentissage, l’utilisateur pourra reconnaître la nature d’un accord, d’après sa forme sur la notation.

Les accord implémentés

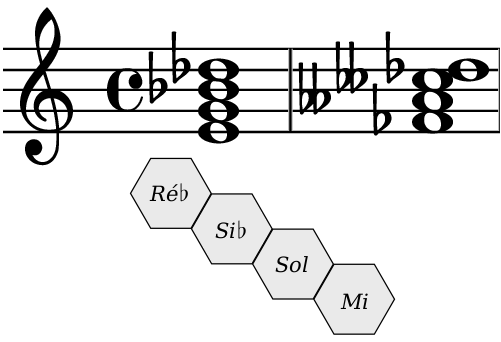
Autre avantage de cette notation, surtout dans une tâche d’apprentissage : deux accords d’une même nature peuvent avoir deux formes différentes dans la notation musicale traditionnelle; on retrouvera quoi qu’il arrive la même forme spécifique dans la notation hexagonale. Sur la figure #ref(fig:trad1), le même accord de 7èmediminuée peut avoir deux formes différentes. Avec la notation de Steedman, cet accord est constitué de quatre hexagones alignés, quelle que soit la tonalité.

Des formes différentes dans la notation musicale, pour le même accord de 7ème.

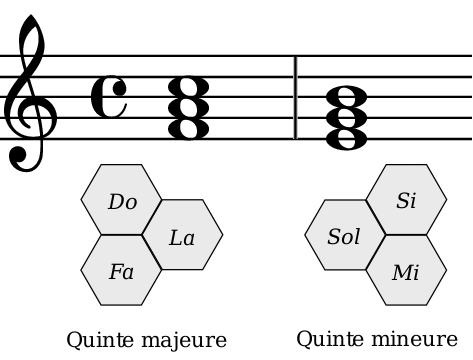
De plus, si deux accords semblent avoir la même forme dans la notation musicale traditionnelle, leurs natures peuvent être différentes. Par exemple, sur la figure @ref, les deux accords se ressemblent. Pourtant, l’un est un accord de quinte majeure, et l’autre un accord de quinte mineure, qui est représenté dans la notation hexagonale par un triangle pointant à droite ou à gauche.

La même forme dans la notation musicale, pour des accords différents : Quinte majeure à gauche, et quinte mineur à droite

5.4.3 Music’haptic : le prototype

D’un point de vue système, le fonctionnement de Music’haptic est schématisé sur la figur 5.28. Nous avons eu recours à des script CGI exécutés sur le serveur, afin de générer les document graphiques (la notation musicale traditionnelle, et les portions de SVG), demandés par les requêtes utilisateurs.

Survol du système

Dans notre prototype, nous nous appuyons sur la représentation de Steedman afin de présenter les différents accords à l’utilisateur.

Deux modes sont disponibles :

• le mode damier : dans ce mode, l’utilisateur peut librement explorer l’ensemble du damier d’hexagones. Chaque note est affichée avec un effet de retour de force, magnétisant le pointeur en son centre (figure 5.29). La note est jouée en même temps.
• le mode accord : ici, l’utilisateur peut isoler un accord, et n’explorer que celui-ci. C’est grâce à ce mode, que l’utilisateur peut progressivement appréhender la forme spécifique à une nature d’accord.

Une note et son retour de force

Le clavier permet de basculer entre les différents modes, ainsi que de choisir l’accord à explorer ou à étudier (quinte majeur, quinte augmentée, etc. voir la figure 5.25).

La dernière possibilité de ce prototype est la génération dynamique des accords sélectionnés, en notation musicale classique (sur une portée, en clé de sol). Ainsi, l’information musicale est disponible sous deux formes visuelles, dont une classique, et ce de manière à permettre l’apprentissage, le partage entre utilisateur de la souris et enseignant (voyant).

Le retour de force sur l’affichage hexagonal, et la notation musicale, dynamiquement générée

5.5 Conclusion

Dans ce chapitre, nous avons présenté notre proposition de contexte d’utilisation d’une souris à retour de force dans un cadre d’accessibilité : la localisation relative, illustrée par la métaphore du levier de vitesse.

Deux protocoles de test nous ont permis d’entrevoir les possibilités et les limites de la localisation relative, à savoir :

• l’approche est probante en terme de mémorisation, tant que le nombre de zones haptiques reste raisonnable (<9);
• l’effet de l’habitude d’utilisation de la souris est important;
• le temps d’exploration sur une surface haptique est linéaire en n.

Nous avons également développé deux applications qui répondent aux critères énoncés et qui exploitent les possibilités de la localisation relative. Pour autant, c’est le périphérique en soi (la souris Wingman), qui limite le plus les prototypes réalisés.

Nous en concluons néanmoins, que la localisation relative est une approche viable, si ce n’est la seule, quant à l’utilisation des périphériques de pointage à retour de force, dans un cadre d’accessibilité.

Bibliographie

Braille music editor [WWW Document], n.d. URL https://braillemusiceditor.com/

Brandao, M., Wiggins, G., Pain, H., 1999. Computers in music education, in: Proceedings of the AISB’99 Symposium on Musical Creativity. AISB (Society for the Study of Artificial Intelligence; the Simulation of …, pp. 82–88.

Castaing, J., 2005. Musicdraw : To make music learning attractive, in: Forth MUSICNETWORk Open Workshop, 2004, Barcelona, Spain.

Edwards, A.D., Holland, S., 1992. Multimedia interface design in education. Springer Science & Business Media.

Faineteau, H., Gentaz, E., Viviani, P., 2003. The kinaesthetic perception of euclidean distance: A study of the detour effect. Experimental Brain Research 152, 166–172.

Fitts, P.M., 1954. The information capacity of the human motor system in controlling the amplitude of movement. Journal of experimental psychology 47, 381.

Gardner, J.A., Bulatov, V., 2001. Smart figures, svg, and accessible web graphics, in: Proceedings of the Technology and Persons with Disabilities Conference.

Holland, S., 2000. Artificial intelligence in music education: A critical review.

Holland, S., 1987. Direct manipulation tools for novices based on new cognitive theories of harmony, in: Proceedings of 1987 International Computer Music Conference. pp. 182–189.

Howell, P., Cross, I., West, R., 1985. Musical structure and cognition.

Hyman, R., 1953. Stimulus information as a determinant of reaction time. Journal of experimental psychology 45, 188.

Longuet-Higgins, H., n.d. 19626 second letter to a musical friend. Music Rev 23, 280.

Longuet-Higgins, H.C., others, 1962. Letter to a musical friend. Music review 23, 244–248.

M. H. Reenskaug, T., 1979. Models-views-controllers.

Siekierska, E., Labelle, R., O’NEIL, L., 2001. Tactile mapping project at canadian federal mapping agency-mapping services branch, in: Proceedings of the 20th International Cartographic Conference, ICC. Citeseer, pp. 6–10.

Steedman, M., 1972. The formal description of musical perception.

Toccata - braill music translation software [WWW Document], n.d. URL https://www.pentronics.com.au/Toccata.html

Zhai, S., Milgram, P., Buxton, W., 1996. The influence of muscle groups on performance of multiple degree-of-freedom input, in: Proceedings of the SIGCHI Conference on Human Factors in Computing Systems. pp. 308–315.

---

12. site web : http://tactile.nrcan.gc.ca/↩︎

13. http://maps.google.fr↩︎

14. http://maps.yahoo.com/↩︎

15. http://local.live.com↩︎